Example 1

Bilinearly constrained nonlinear program:

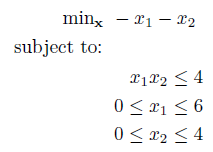
The above problem contains a linear objective function, but a bilinear inequality constraint which infers a NLP (or technically a QCLP). To solve this using BARON, first write anonymous functions for the objective and constraint. Then, declare the constraint and decision variable bounds:

% Objective Function
fun = @(x) -x(1) - x(2);

% Nonlinear Constraints
nlcon = @(x) x(1)*x(2); %note we could also use prod(x)
cl = -Inf;
cu = 4;

% Bounds
lb = [0;0];
ub = [6;4];

This can be solved using BARON as follows:

x = baron(fun,[],[],[],lb,ub,nlcon,cl,cu)

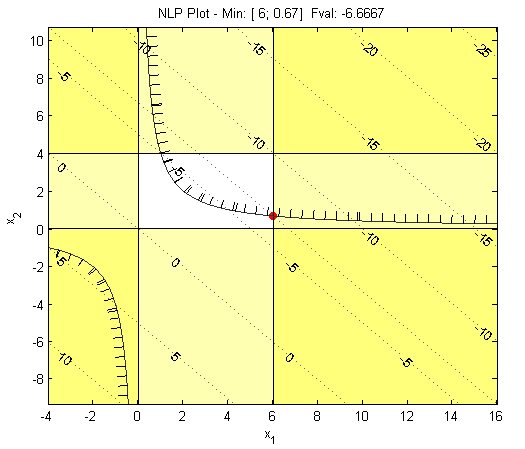
And the solution is:

x =

6.0000
0.6667

Using MATLAB's plotting functions for two- (or sometimes three-) dimensional problems it can be useful to plot the objective, constraints, and solution:

The MATLAB/BARON interface is provided at http://www.minlp.com. The interface is provided free of charge and with no warranties.