Example 3

Nonlinearly constrained mixed-integer nonlinear program:

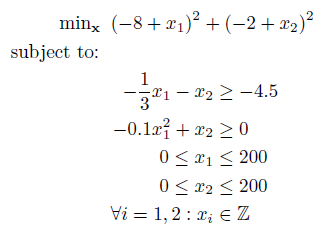
The above problem contains a quadratic objective function with one linear and one quadratic constraint. There is an additional constraint where all decision variables must be integers, making this a mixed-integer nonlinear programming problem (or technically a MIQCQP). As with previous examples, create anonymous functions for the objective and constraints. However, note that we can enter the linear constraint as a matrix of the form rl ≤ Ax ≤ ru:

% Objective
a = [-8;-2];
fun = @(x) sum((a+x).^2); %note the use of vectorized commands

% Linear Constraints
A  = [-1/3 -1];
rl = -4.5;
ru = Inf;

% Nonlinear Constraints
nlcon = @(x) -0.1*x(1)^2 + x(2);
cl = 0;
cu = Inf;

% Bounds
lb = [0;0];
ub = [200;200];

% Integer Constraints
xtype = 'II';

This can be solved using BARON as follows:

[x,fval,exitflag,info] = baron(fun,A,rl,ru,lb,ub,nlcon,cl,cu,xtype)

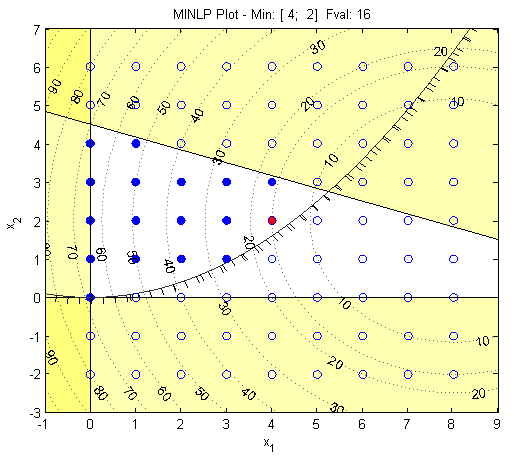
The solution is:

x =

4
2

Using MATLAB to plot the solution, we can view the problem:

The MATLAB/BARON interface is provided at http://www.minlp.com. The interface is provided free of charge and with no warranties.